Neoclassical Axioms and their Effect on Individual Preferences

By: Julian Olsen-Pendergast

The process of understanding individual preference and by extension consumer demand behaviour is fundamental to economic choice theory. The neoclassical school of economic thought proposed a set of independent assumptions, to help economists understand individual preferences and the decisions rational individuals make between alternative consumption choices. These assumptions, known as axioms, are fundamental to neoclassical consumer demand behaviour theory. This essay presents these axioms, demonstrates their relevance to individual’ preference and analyses whether consumer demand behaviour always satisfies these axioms.

The first neoclassical axiom of individual preference is completeness. The axiom of completeness states that a preference ordering is only complete once it allows the consumer/individual to place all bundles or combinations of goods and services in a discrete order of preference. In other words, the consumer must be able to rank all the available bundles, however unlike or like they are. If individual one is presented with two bundles, x and y, he/she must be able to make one of three statements: they prefer buddle x to bundle y, they prefer bundle y to bundle x or they are indifferent between bundle x and bundle y. An example of an individual violating this axiom is the statement ‘they’re so different, I can’t choose’. The individual does not satisfy the neoclassical axioms placed on individual preference and is therefore an irrational individual. (Frank & Cartwright, 2020)

The second neoclassical axiom of individual preference is transitivity. The axiom of transitivity, or a consistency requirement, states that if an individual is presented with bundles x, y and z, if he-she prefers x to y and he-she prefers y to z, then he-she must prefer x to z. If this is not the case, the axiom of transitivity is violated. If this axiom was not in place it would lead to a cycle referred to as a ‘money pump cycle’ (Frank & Cartwright, 2020). This would occur if an individual preferred x to y and y to z, but also preferred z to x. When given z, he/she would trade it for y, which he/she would trade it for x, which he-she would then trade for z. This results in an infinite loop of trade. Furthermore, if there is a transaction cost associated with trade, he/she would trade until they had nothing left.

The third neoclassical axiom of individual preference is reflexivity. The axiom states that any bundle presented is at least as good as or indifferent to itself. However seemingly inconsequential it appears to be it is important in certifying that every buddle available belongs to at least one indifference set, specifically that it accommodates itself and that preferences are consistent over time. An example of this axiom being violated is the statement ‘Whichever I choose I know I’ll be sorry’. This violates the axiom due to a perceived preference change in the future. If an individual prefers x to y at time 1, and then prefers y to x at time 2. It implies that this individual prefers x to x. Therefore, the individual is being irrational and thus, does not satisfy the third axiom. (Gravelle & Rees, 1992)

The three axioms above allow bundles of goods and/or services to be placed into a ranked list from ‘best’ to ‘worst’ which is known as a preference relation R that provides a weak preference ordering. This list is a weak preference ordering due to the individual potentially being indifference between some bundles, i.e., tied on the ranked list.

The fourth neoclassical axiom of individual preference is the axiom of greed. Otherwise known as the assumption of non-satiation, it states that, ceteris paribus, more of a good or service is preferential to less. For example, if individual one has the choice of bundle A (x1, y1) and B (x2, y2), containing two goods x and y. If x1 > x2 and y1 > y2, then he/she will always choose buddle A. This is only the case if the good or service in question is not ‘bad’, for example airplane noise. However, what if an individual has gone to a wedding with a free buffet and eats a lot. He/she may feeling sick from eating too much. In cases like this the economic theory of free disposal can be stated, in which captured goods that are costless may be costlessly thrown away (Andres ́ Salamanca 2016). Thus, in the case you have , much food, one can simply not eat the excess. This axiom can only be violated if free disposal theory is negated, this would be due to a potential self-control complication, not a disproof of the axiom. (Green, 1976)

The fifth neoclassical axiom of individual preference is the axiom of continuity (see figure 1 below). Assume that along the line the connects point W and point Z. Along the line there are infinite combinations of good x and good y, for example B. Given Z is preferred to A (axiom of greed), and A is preferred to W (axiom of greed). Therefore, there must be a point along the line that connects the two points (W and Z) that individual 1 is indifferent on to A i.e., the tipping point between not preferred and preferred. In this case B is that such point. Using the axiom of greed, we can assume that there will only be one such buddle along the line that satisfies the condition of being indifferent upon to A. This can be taken a step further as we can assume that there must be more points on the diagram that have the same utility i.e., where individual 1 is indifferent upon. One of these points is C. If this process is repeated one can create an indifference curve. An indifference curve is a curve made up of infinite points that individual 1 is indifferent upon. Additionally, this implies that the indifference curve has no gaps or breaks at any point. (Frank & Cartwright, 2020)

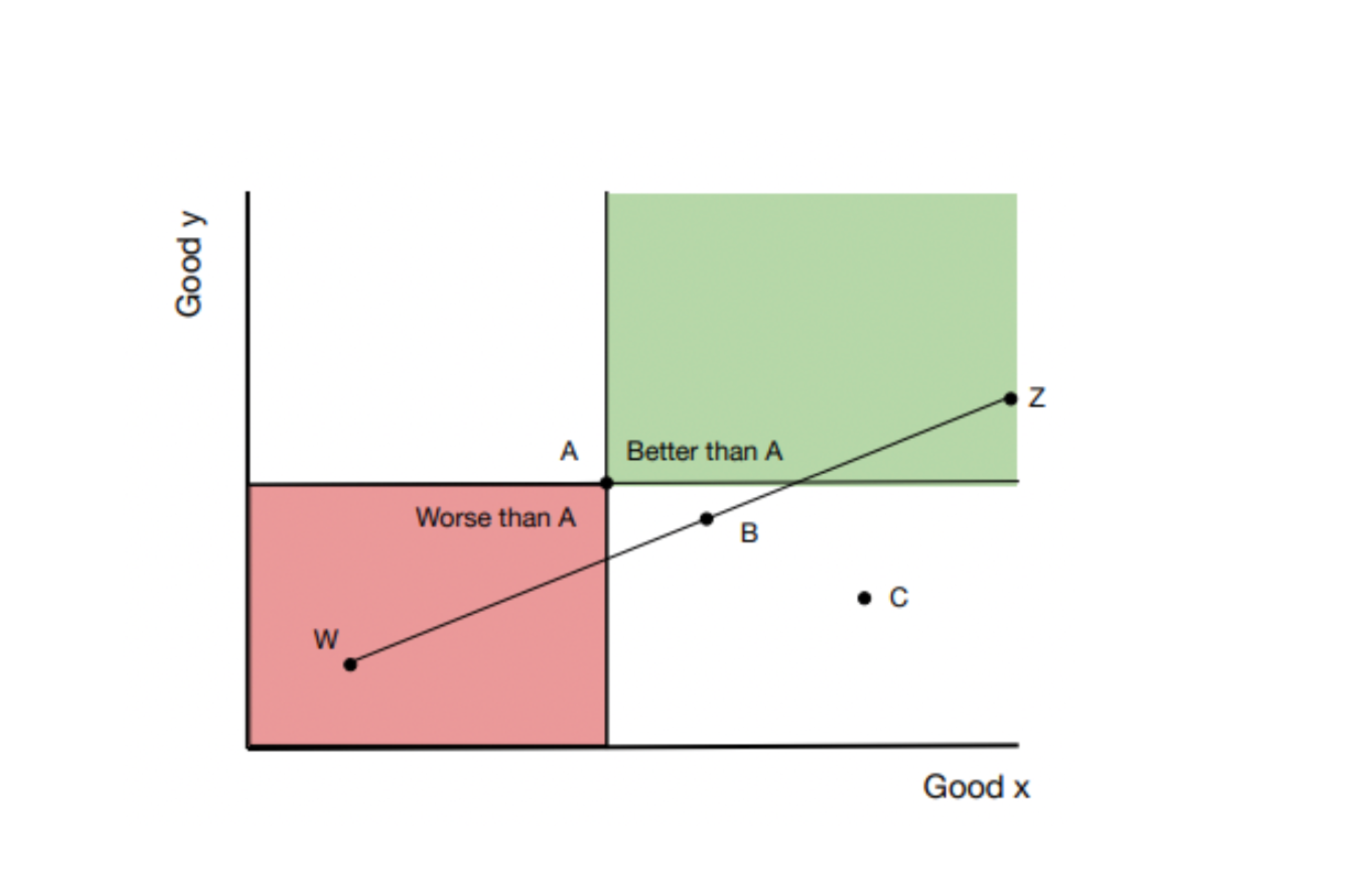
The significance of the axiom of continuity and the axiom of greed is that we can now place restrictions on the surface of indifference curves. Using these axioms it can imply three restrictions. Firstly, a rational individual will always choose an affordable bundle on the highest indifference curve, i.e., where the curve touches the budget constraint, thereby maximising their utility. Secondly, this implies that the indifference curves are lines not areas. Lastly, it means that indifference curves always slope downward.

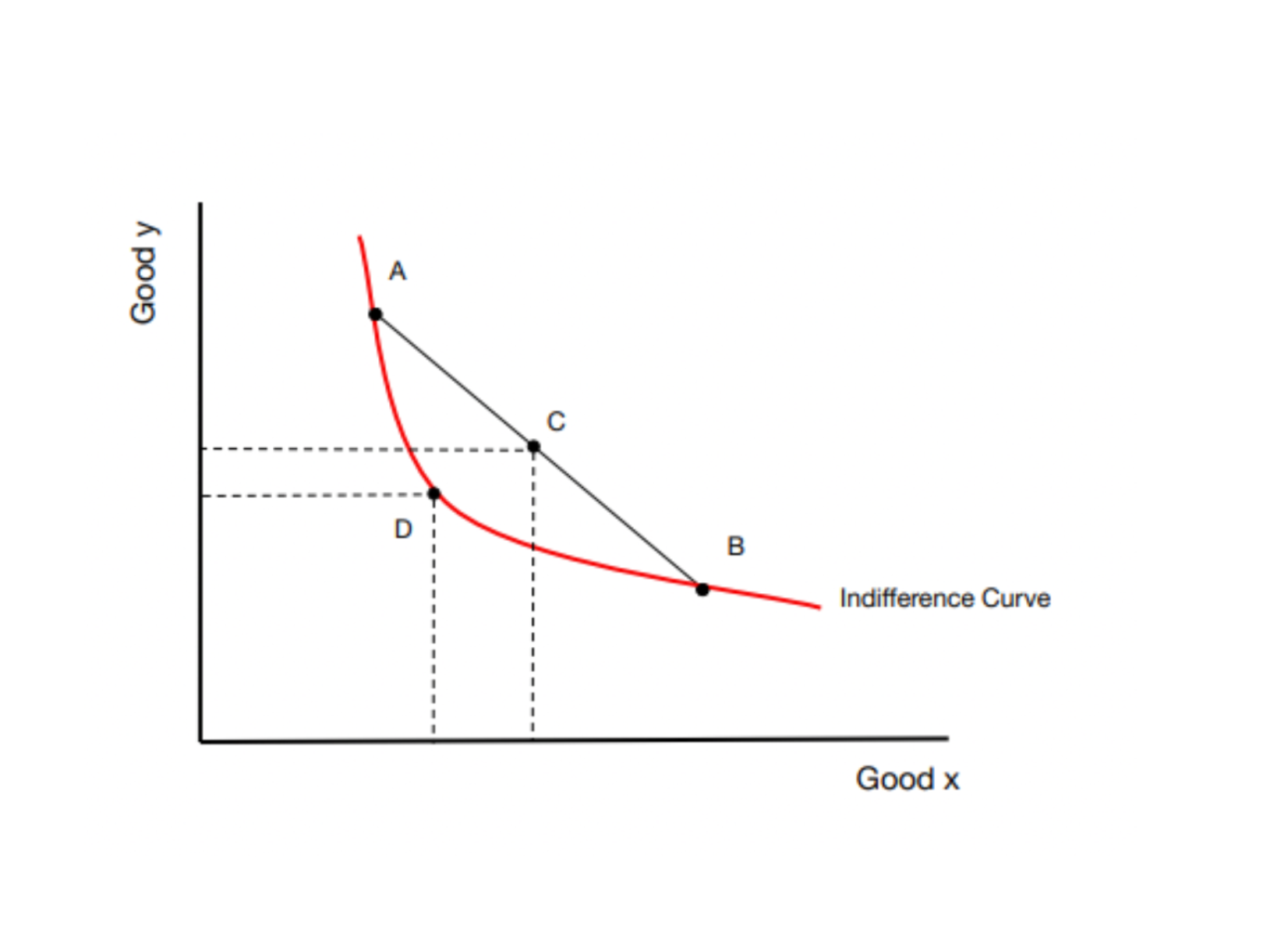
Lastly, the sixth neoclassical axiom of individual preference is the axiom of strict convexity. Under the axiom of strict convexity individuals will prefer a combination of goods rather than lots of one good (see figure 2). In figure two, individual 1 is indifferent upon points A, B, and D, Point C is preferred to A, B, D. The axioms states that along all possible equal consumption points (indifference curve), the more of good x individual 1 has the more of good x they are willing to give up to get a unit of good y. The marginal rate of substitution (the amount of a good a consumer is willing to forgo to consume another good, yielding the same overall utility) increases as one moves up to the left. The indifference curve is convex towards the origin as consumer choice is driven by diminishing marginal rate of substitution (Gravelle & Rees, 1992). Individuals like variety in consumption of goods x and y. If good x is glasses of water and good y is DVDs, a rational individual would prefer a mix of DVDs and water.

A key question remains - does rational consumer demand behaviour always satisfy the neoclassical axioms? If we assume consumer demand behaviour is the behaviour of a perfectly rational consumer’s demand. Are their consumption choices always consistent with the axioms of neoclassical preference? Some economists argue that consumers can be rational and at the same time violate axioms.

The simplest axiom that if broken does not mean that the individual is irrational is completeness. Under the axiom, the individual is expected to rank all preferences. However, some characteristics of goods may not be clear or there is imperfect information. This is manifested when individuals are asked a question for a utility function elicitation, and their answers are not precise (Anand, 1987). It is therefore reasonable to expect that consumers can be imprecise and violate the axiom of completeness, and yet remain inherently rational.

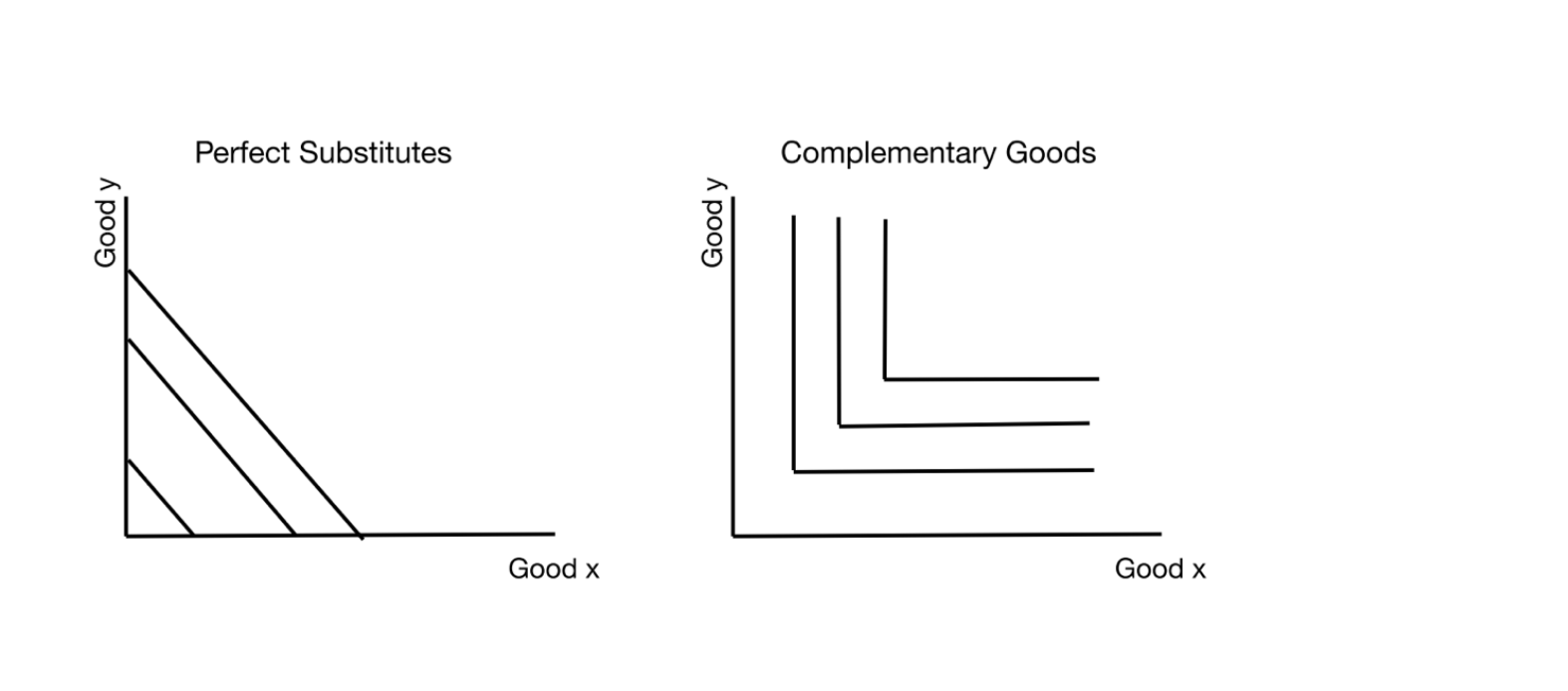
Secondly, the axiom of strict convexity can be broken by a rational individual. If an individual is stranded on a desert island without fresh water, he/she (rational consumer) would not want a combination of bottles of water and DVDs. A rational consumer would have extremely high utility from consumption of water, i.e., preventing dying of dehydration, and no utility from DVDs. Thus, breaking the axiom of strict convexity. Furthermore, the axiom does not consider if two goods that are perfect substitutes. The relationships between goods that are substitutes and its indifference curves is shown in figure 3. The MRS of the goods x and y is not subject to the law of diminishing marginal utility the same way as two normal goods. Therefore, not strictly convex.

Lastly, the axiom of continuity can be violated, and the consumer is still rational. If the two goods that make up the buddle are complementary goods. In the case of complementary good the shape of their indifference curve is like an L (figure 3). For example, looking at left shoes and right shoes. Having 3 left shoes and 2 left shoes is no better than having 2 left and right shoes. Therefore, the indifference curve shaped like an L. (Green, 1976)

However, given the axioms use in simple models with bundles of two goods or services that don’t factor in time, one can assume that apart from select cases consumer demand behaviour consistently satisfies the neoclassical axiom of completeness. Furthermore, the violating of the axiom of continuity can be addressed if the individual treats pairs of shoes as the commodity unit and thus only counts complete pairs. Lastly, even on a desert island the rational individual 1 could have too much water and potentially have some use for the DVD’s, i.e., alerting ships.

To conclude, individual choice under the neoclassical school of thought and by extension the preferences the individuals make can be summarised into six axioms. These axioms allow economist to understand a analyse consumer behaviour when it comes to consumption and demand. Primarily, a rational consumer will consistently abide by these assumptions, however, under some specific and niche scenarios they break the axioms and remain rational. Nevertheless, these scenarios are few and far between and not directly applicable to simple two good preference ordering models.